Weibullovo rozdělení

Weibullovo rozdělení je spojité rozdělení pravděpodobnosti. Jméno nese po švédském matematikovi Waloddim Weibullovi, který jej podrobně popsal v roce 1951, ačkoli bylo poprvé identifikováno Fréchetem (1927) a poprvé použito Rosinem a Rammlerem (1933) k popisu distribuce velikosti částic.

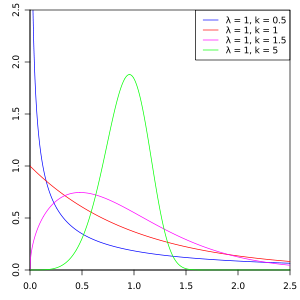
Hustota pravděpodobnosti Weibullovy náhodné veličiny je:^[1]

${\displaystyle f(x;\lambda ,k)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}&x\geq 0,\\0&x<0,\end{cases}}}$

kde k > 0 je parametr tvaru a λ > 0 je měřítko distribuce. Weibullova distribuce souvisí s řadou dalších distribucí pravděpodobnosti; zejména leží mezi exponenciálním rozdělením (k = 1) a Rayleighovým rozdělením (k = 2 a ${\displaystyle \lambda ={\sqrt {2}}\sigma }$^[2]).

V lékařské statistice a v ekonometrii se používá jiná parametrizace.^[3][4] Parametr tvaru k je stejný jako výše a parametr měřítka je ${\displaystyle b=\lambda ^{-k}}$.

Někdy se používá i třetí parametrizace, kdy je parametr tvaru k opět stejný jako výše a parametr měřítka je ${\displaystyle \beta =1/\lambda }$.

Kumulativní distribuční funkce pro Weibullovo rozdělení je

${\displaystyle F(x;k,\lambda )=1-e^{-(x/\lambda )^{k}}\,}$

pro x ≥ 0 a F ( x ; k ; λ) = 0 pro x <0.

Kvantilová funkce (inverzní kumulativní distribuční) funkce pro Weibullovo rozdělení je roztažená exponenciální funkce.

${\displaystyle Q(p;k,\lambda )=\lambda (-\ln(1-p))^{1/k}}$

pro 0 ≤ p <1.

Weibullova distribuce se používá

• V analýze přežívání
• V analýze spolehlivosti a poruch
• V elektrotechnice může reprezentovat přepětí vyskytující se v elektrickém systému
• V průmyslovém inženýrství k popisu výrobních a dodacích lhůt
• V teorii extrémních hodnot
• V oblastech předpovídání počasí a větrné energetiky popisuje rozdělení rychlosti větru, protože přirozené rozdělení často odpovídá Weibullovu tvaru^[5]
• V inženýrství komunikačních systémů
  • V radarových systémech modeluje rozptyl úrovně přijímaných signálů produkovaných některými typy rušení
  • K modelování fadingu v bezdrátových komunikacích, protože se zdá, že Weibullův model vyhovuje experimentálním měřením zeslabování signálu
• V analýze vyhledávání informací modeluje dobu setrvání uživatelů na webových stránkách.^[6]
• V oblasti pojištění bylo Weibullovo rozdělení použito k modelování velikosti pojistných nároků na zajišťovny a kumulativního vývoje ztrát z azbestózy
• Při předpovídání technologických změn (model Sharifa-Islama)
• V hydrologii se Weibullova distribuce aplikuje na extrémní události, jako jsou roční maximální jednodenní srážky a průtoky řek.
• Při popisu velikosti částic generovaných mletím a drcením se používá dvouparametrická Weibullova distribuce, a v těchto aplikacích je někdy známá jako Rosinova-Rammlerova distribuce. V této souvislosti předpovídá méně jemných částic než log-normální rozdělení a je obecně nejpřesnější pro úzké distribuce velikosti částic. Interpretace kumulativní distribuční funkce je, že ${\displaystyle F(x;k,\lambda )}$ je hmotnostní zlomek částic s průměrem menším než ${\displaystyle x}$, kde ${\displaystyle \lambda }$ je střední velikost částic a ${\displaystyle k}$ je míra rozptýlenosti velikosti částic.
• Při popisu mraků náhodných bodů (jako jsou polohy částic v ideálním plynu): pravděpodobnost nalezení nejbližšího souseda ve vzdálenosti ${\displaystyle x}$ od dané částice je dána Weibullovou distribucí s ${\displaystyle k=3}$ a ${\displaystyle \rho =1/\lambda ^{3}}$ rovným hustotě částic.

V tomto článku byl použit překlad textu z článku Weibull distribution na anglické Wikipedii.

• Obrázky, zvuky či videa k tématu Weibullovo rozdělení na Wikimedia Commons