Čtverečná soustava
V dnešním světě je Čtverečná soustava téma, které vyvolává velký zájem a debatu. Ať už v akademické, profesní nebo osobní oblasti, Čtverečná soustava se stal relevantním a aktuálním tématem. Od svého vzniku až po dopad na dnešní společnost Čtverečná soustava vytvořil širokou škálu názorů a pohledů. V tomto článku prozkoumáme různé aspekty související s Čtverečná soustava, od jeho historického pozadí až po jeho vliv na populární kulturu. Kromě toho probereme důsledky a výzvy, které Čtverečná soustava představuje v různých kontextech, a také možná řešení a přístupy k jejich řešení. Připojte se k nám na této prohlídce fascinujícím světem Čtverečná soustava!
| Tetragonální soustava | |
|---|---|
 | |
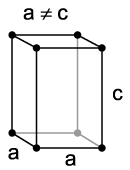| Metrika | a=b≠c, α=β=γ=90° |
| Bravaisovy mřížky | P, I |
| Souměrnost | střed souměrnosti, čtyřnásobná osa souměrnosti, čtyři dvojnásobné osy, pět rovin souměrnosti |
| Bodové grupy | holoedrická mmm, hemiedrické 4/m, 4mm, 422, 42m, 4 a 4 |
| Krystalové tvary | pedion, pinakoid, ditetragonální dipyramida, ditertagonální pyramida, tetragonální dipyramida, tetragonální pyramida, tetragonální skalenoedr, tetragonální traperzoid a tetragonální disfenoid |
Čtverečná, tetragonální soustava je jedna ze sedmi krystalografických soustav. Možné prvky souměrnosti jsou: čtyřnásobná osa souměrnosti (symbol 4), čtyři dvojnásobné osy (2), maximálně pět rovin souměrnosti (m), střed souměrnosti (1) a jejich kombinace. Bravaisovy mřížky jsou zastoupené dvě: primitivní (P) a prostorově centrovaná (I).
Typy mřížek
-
Primitivní mřížka -
Prostorově centrovaná mřížka
Výběr souřadnicové soustavy
Jako vertikála souřadnicové osy Z se vybírá čtyřnásobná osa (4), případně inverzní čtyřnásobná osa (4). Jak jsou na ni kolmé dvojnásobné osy, dvě z nich jsou potom osami X a Y. Pokud nejsou přítomné dvojnásobné osy souměrnosti, je tu možnost vybrat tyto souřadnicové osy X a Y ležící v rovinách souměrnosti. V případě, že nejsou přítomné ani roviny, tak je výběr os X a Y nevázaný a standardní orientace je taková, aby měl dominantní krystalový tvar Millerovy symboly {hkl}, nebo {110}.
Krystalové tvary
V jednotlivých grupách jsou možné další tvary:
- mmm - pinakoid, tetragonální prizma, tetragonální dipyramida, ditetragonální prizma, ditetragonální dipyramida
- 4/m - pinakoid, tetragonální prizma, tetragonální dipyramida
- 4mm - pedion, tetragonální prizma, tetragonální pyramida, ditetragonální prizma, ditetragonální pyramida
- 422 - pinakoid, tetragonální prizma, tetragonální dipyramida, ditetragonální prizma, tetragonální traperzoedr
- 42m - pinakoid, tetragonální prizma, tetragonální dipyramida, ditetragonální prizma, tetragonální disfenoid, tetragonální skalenoedr
- 4 - pedion, tetragonální prizma, tetragonální pyramida
- 4 - pinakoid, tetragonální prizma, tetragonální disfenoid
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Tetragonálna sústava na slovenské Wikipedii.
Externí odkazy
Obrázky, zvuky či videa k tématu Čtverečná soustava na Wikimedia Commons
Krystalový tvar na webu mineralogie.sci.muni.cz (Václav Vávra, Zdeněk Losos; Ústav geologických věd, Přírodovědecká fakulta Masarykova univerzita, Brno)
